1. Vectores:
componentes
El vector es
una representacón gráfica de una magnitud física que posee ademas de
tamaño, dirección y sentido, es necesario poder representar las magnitudes de tipo vectorial, se a considerado que mediante la utilización de un vector es la mejor manera de poder operarlo. Por tanto toda magnitud vectorial se representa a traves de un vector. a continuación en la figura de aprecia los componentes de un vector.
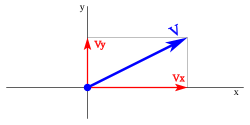
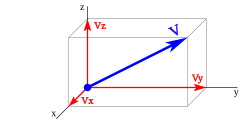
En coordenadas cartesianas. Coordenadas en tres dimensiones.
Existe dos formas de representar un vector:
1) Forma polar.- se representa con el modulo y el angulo.
2) Sistema coordenadas.- se descompone sobre le eje x,y. que notamos en las figurar anterioes
Tambien al vector se le considera un segmento dirigido.
Puedes leer este texto interesante aqui.
2. Vector unitario
Es un vector cuyo modulo es la unidad, tan simple como eso, a este vector se le suele representar con un acento cincunflejo (un sombrerito, puedes revisar la monografia para enterarte mas de tal acento, pero no es misión en este caso). Si tuvieramos un vector  , su vector unitario se representa asi:
, su vector unitario se representa asi:  , actualmente se utiliza la letra
, actualmente se utiliza la letra  para representar lo mismo.
para representar lo mismo.
 , su vector unitario se representa asi:
, su vector unitario se representa asi:  , actualmente se utiliza la letra
, actualmente se utiliza la letra  para representar lo mismo.
para representar lo mismo.Para un caso mas general, sea el vector
 , para obtener el vector unitario se procede a dividir el vector entre su módulo.
, para obtener el vector unitario se procede a dividir el vector entre su módulo.
Se lee vector unitario de 

Nota: Al vector unitario de un vector tambien suele llamarse versor de un vector, y en otros casos vector normalizado. Tener cuidado con las denominacione spor si los sorprenden.
3. Producto escalar (Producto punto, interno o interior)
Es una multiplicacion entre dos vectores cuyo resultado será un número o escalar. Geometricamente podemos representar de la siguiente forma: sean los vectores A y B.
|A| cos(θ) es la proyección escalar de A en B.
Para hallar el angulo despejamos:
Si el angulo formado es 90º,
Propiedades: El producto escalar cumple con la propiedad conmutativa, distributiva y asociativa.
4. Producto vectorial (producto cruz)
Esta operacion entre dos vectores da como resultado un nuevo vector que es perpendicular a los anteriores.
Observaciones: axb es diferente que bxa, el producto vectorial no cumple la propiedad conmutativa. para hallar la direccion del vector resultante podemos usar la regla de la mano derecha.
Fuente: pVectorial / pEscalar
5. Operaciones
gráficas y analíticas
Resta de vectores: Tambien sera otro vector que presenta la caracteristica de la figura siguiente :
Multiplicacion por un escalar: Es otro vector cuyo modulo sera el multiplicado por ese escalar. Si el escalar es negativo el vector tendra la misma dirección pero el sentido contrario, como se muestra en al siguiente figura.
6. Función: recta y parábola
Funcion de la recta o lineal.- Es una funcion que se representa a traves de un linea continua en el plano cartesiano, tambien se le conoce como funcion polinomial de primer grado y tiene la siguiente forma:
Veamos dos ejemplos:
Funcion parábola.- Tambien conocida como funcion cuadrática tiene las siguientes caracteristicas.
Es de la forma: f(x) = ax2 + bx + c
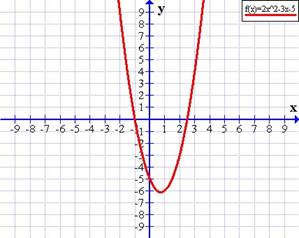
Si a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x2 − 3x − 5
Si a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2 + 2x + 3
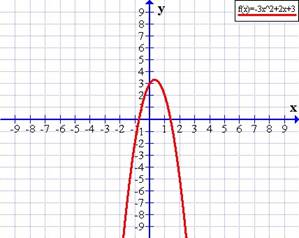
Veamos dos ejemplos:
Vemos en el plano cartesiano la representacion de dos rectas, una con m=0.2 y otra con pendiente negativa -1.
Funcion parábola.- Tambien conocida como funcion cuadrática tiene las siguientes caracteristicas.
Es de la forma: f(x) = ax2 + bx + c
Donde a,b,c, son números reales y a es distinto de cero, esta compuesto por tres partes, el término cuadrático, el término lineal y el término independiente. La representación grafica se da a continuación.
Si a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x2 − 3x − 5
Si a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x2 + 2x + 3



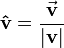






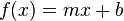

No hay comentarios:
Publicar un comentario