Muchos movmientos se pueden considerar que se realizan en un plano, uno de los ejemplos mas conocidos son el caso de los proyectiles, este se estudiará mas adelante. Como se va a considerar la aceleracion constante en este movimiento, los componentes en su eje no varian, podemos determinar la ubicacion de una particula en el plano a traves del vector posicion, la imagen a continuación aclara lo mencionado. Es bueno precisaar que las ecuaciones del movimiento seran los mismos que el caso de MRUV, solo que aqui el movmiento sera tanto en el eje x y el eje y. Existe aceleración en los dos ejes. Es como aplicar MRUV en ambos ejes.
Fuente: MovDosDimensiones
2. Movimiento de proyectiles (Movimiento Parabólico)
Este tipo de movimiento lo puedes observar si lanzas un objeto, veras que tiene una trayectorial caracteristica (una curva), similar a una parabola invertida, porque ocurre esto, porque todos los cuerpos en la tierra son atraidas a esta, entonces en todos el movimiento la gravedad tira hacia abajo, tratando de modificar su movimiento a cada instante, variando su velocidad hasta que llega al suelo, podemos ver que el objeto alcanza una altura maxima, cuando su velocidad tiende a cero, para luego continuar su caida.
Debemos asumir estas condiciones para facilitar el analisis:
1)La gravedad de la tierra es constante en todo el intervalo del movimiento.
2) Se desprecia el efecto de la resistencia dinámica del aire.
La ecuaciones del movimientos sera:
En el eje x se considera que la particula desarrolla un MRU, osea la velocidad en el eje horizontal el constante y la distancia recorrida se obtiene aplicando la formula de d=vt.
En el eje y, la particula se ve afectada por la aceleración de la gravedad (g), entonces se hara uso de la ecuacion de MRUV,por tanto la velocidad e el eje y va cambiado constantemente. tener cuidado con los signos, suele ser un error muy comun. la gravedad sera negativa porque apunta siempre abajo, considerando el sistema cartesiano de coordenadas. Miremos la grafica siguiente para darnos una idea.

Fuente: Mov.EnElPlano
Demostracion de las ecuaciones.
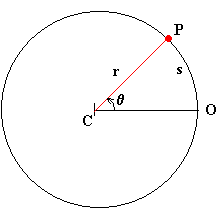
Este movimiento esta basado en el traslado de una particula alrededor de un punto llamado eje y cuya trayectoria es una circunferencia, se definirán los siguientes terminos:
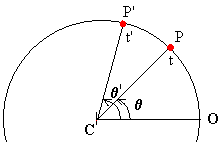
Posición Angular .- Es el angulo que hace desde el origen de angulo O, hasta una posición cualesquiera. Se define a este angulo como el cociente longitud de arco y radio de la circunferencia.
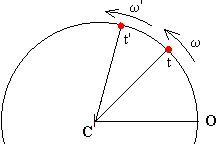
Velocidad Angular (w) .- La velocidad de un punto se evaluará conforme vaya cambiando de angulo, entonces la velocidad angula expresa la variación de angulo recorrido sobre un intervalo de tiempo.
Aceleración Angular (a) .- Definida como el cociente entre el cambio de velocidad angular en un intervalo de tiempo.
4. Movimiento circular uniforme (MCU)
En este caso la velocidad angular es constante, por consiguiente la aceleracion angular es cero. Normalmente el t inicial se toma desde cero. La ecuaciones para este movimineto seran.
Aqui la aceleración angular es constante, como sabemos esta aceleración se determina de la variacion de la velocidad angular en determinado instante. Las ecuaciones para este movmiento son:
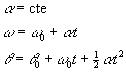
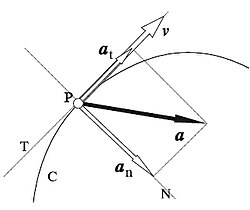
A diferencia de la velocidad que es tangente a la trayectoria de una partícula, la aceleración no lo es, sin embargo esta se puede descomponer (componentes intrínsecas), estas componente seran perpendiculares entre si, una componente tangencial at , esta es tangente a la trayectoria, denominada aceleración tangencial, y una componente normal an, esta es normal a la trayectoria, tambien llamada aceleración centrípeta, por siempre apuntar al centro de curvatura.
La ecuaciones para at y an
7. Velocidad relativa
Se dice que la velocidad de una particula es relativa, porque depende del observador, veamos si una persona viaja en autobus, para un observador que se encuentra en el autobus esta persona no tiene velocidad, osea su velocidad es cero, sin embargo para un observador en tierra esta persona se mueve con cierta velocidad, por eso se dice que la velocidad depende o es relativo a un observador, tambien podemos decir depende de donde se encuentre el sistema de referencia del observador.
En esta seccion no hay formulas, aqui se trata de observar e intuir las distintas velocidades. Si tenemos dos moviles A y B, se dice que la velocidad relativa de A con respecto a B.
Para el caso inverso, velocodad de B respecto de A.
Nota: El estudio de estas velocidad relativa puede crear ciertas confusiones, porque a veces tratatos de aplicar formulas y no las hay solo mera deducción, se que es un tema amplio que se debiera abordar con mas explicaciones, ojala pueda hacerlo mas adelante...



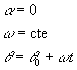

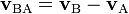
No hay comentarios:
Publicar un comentario